|
TI-Nspire CX
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Geometry 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
価格 |
|
|
|
TI-Nspire CX
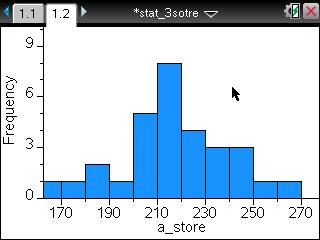
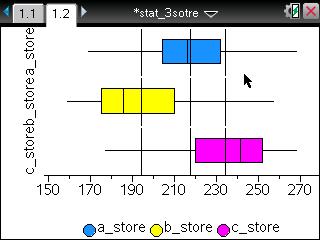
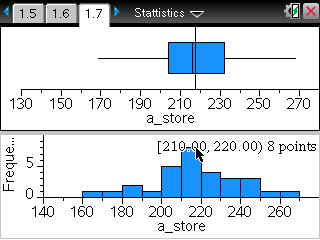
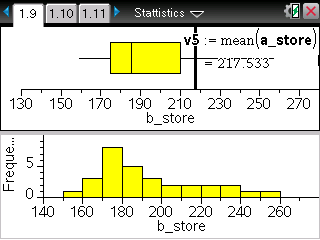
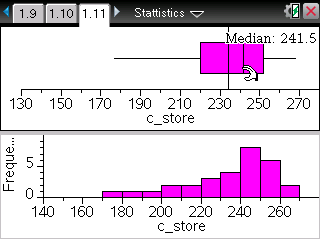
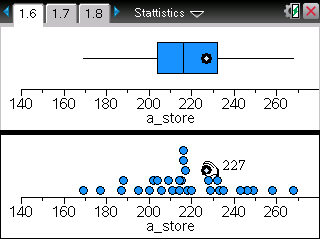
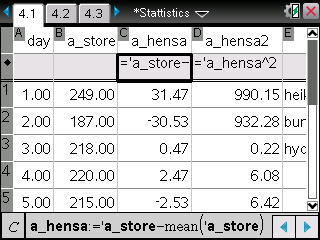
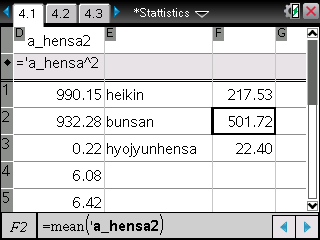
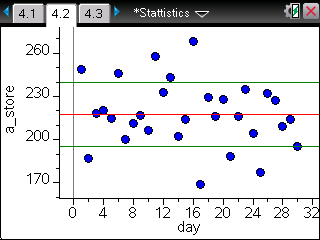
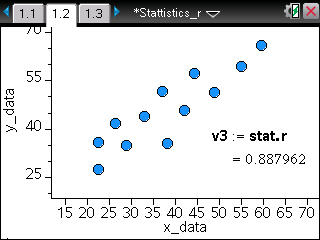
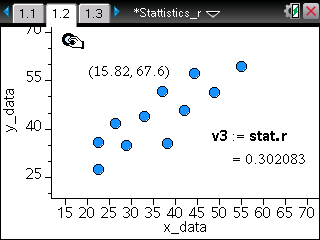
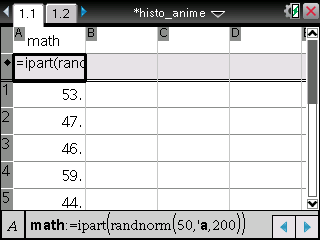
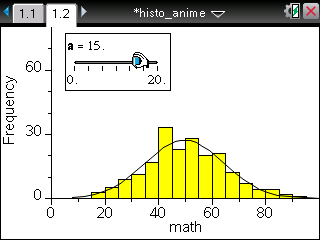
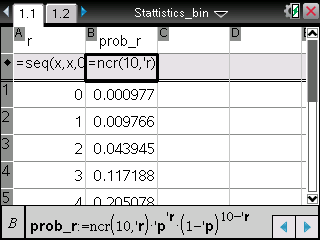
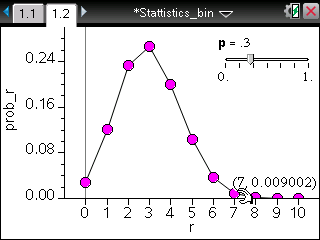
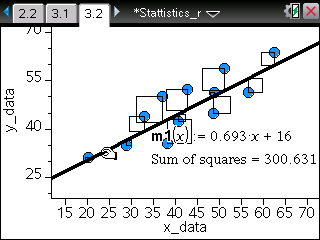
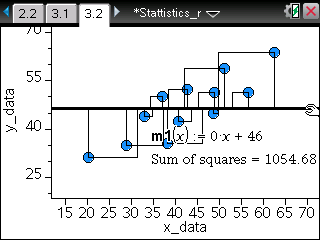
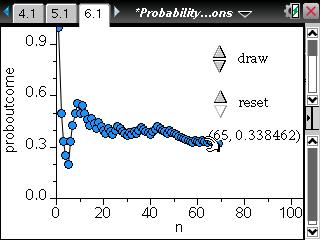
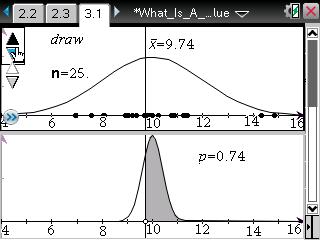
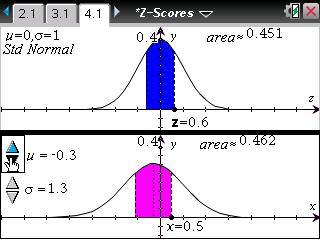
TI-Nspire ― Spreadsheet / Data & Statistics
TI-Nspire CX
![]()
TI-Nspire CX
下の画面を動かすことができます。画面をクリックするか、下記のタイトルをクリックしてください。
TI-Nspire CX
|
|
|
|
|
|
|
|
TI-Nspire CX
![]()
TI-Nspire CX
![]()
Copyright 1998-2014 Naoco Incorporated. All right reserved.